
ค่าเฉลี่ยเคลื่อนที่เป็นหนึ่งในตัวชี้วัดทางเทคนิคที่ล่าช้า ซึ่งผู้เทรดและนักลงทุนใช้ในการกำหนดทิศทางของแนวโน้ม
โดยจะรวมจุดข้อมูลของความมั่นคงทางการเงินใดๆ แล้วหารยอดรวมด้วยจำนวนจุดข้อมูลในช่วงเวลาหนึ่งเพื่อให้ได้ค่าเฉลี่ย
เรียกว่า “ค่าเฉลี่ยเคลื่อนที่” เนื่องจากมีการคำนวณใหม่อย่างต่อเนื่องซึ่งอิงตามข้อมูลราคาล่าสุด
นักวิเคราะห์ใช้ค่าเฉลี่ยเคลื่อนที่เพื่อกำหนดแนวรับและแนวต้านโดยการประเมินการเคลื่อนไหวของราคาสินทรัพย์
ตัวบ่งชี้นี้แสดงการเคลื่อนไหวของราคาก่อนหน้าของหลักทรัพย์ที่ผู้ค้าใช้เพื่อกำหนดทิศทางที่เป็นไปได้ของราคาสินทรัพย์
1. ค่าเฉลี่ยเคลื่อนที่อย่างง่าย:
SMA เป็นค่าเฉลี่ยเคลื่อนที่ที่ง่ายที่สุดที่ได้มาจากการเพิ่มชุดข้อมูลล่าสุด แล้วหารผลรวมด้วยจำนวนช่วงเวลา
อินดิเคเตอร์ SMA ใช้สำหรับผู้ค้าเพื่อสร้างสัญญาณว่าเมื่อใดควรเข้าหรือออกจากหุ้น
SMA เป็นอินดิเคเตอร์ที่ล้าหลังเนื่องจากอิงตามข้อมูลราคาในอดีตในช่วงเวลาที่กำหนด ซึ่งสามารถคำนวณราคาประเภทต่างๆ เช่น สูง ต่ำ เปิดและปิด
ผู้เทรดใช้อินดิเคเตอร์นี้เพื่อกำหนดสัญญาณซื้อ ขายสำหรับหลักทรัพย์ และยังช่วยในการระบุโซนแนวรับและแนวต้าน
ตัวอย่างเช่น ผู้เทรดต้องการคำนวณค่าเฉลี่ยเคลื่อนที่อย่างง่ายสำหรับหุ้นโดยใช้ราคาปิดในช่วงห้าวันที่ผ่านมา
ราคาปิดในช่วงห้าวันที่ผ่านมามีดังนี้: Rs.23, Rs.23.40, Rs.23.20, Rs.24 และ Rs.25.50 SMA จะถูกคำนวณดังนี้:
SMA = (Rs.23 + Rs.23.40 + Rs.23.20 + Rs.24 + Rs.25.50) / 5
SMA = Rs.23.82
SMA ของ 9 ช่วงเวลาสุดท้ายของNifty 50ถูกวาดเป็นเส้นบนแผนภูมิราคาที่แสดงด้านล่าง: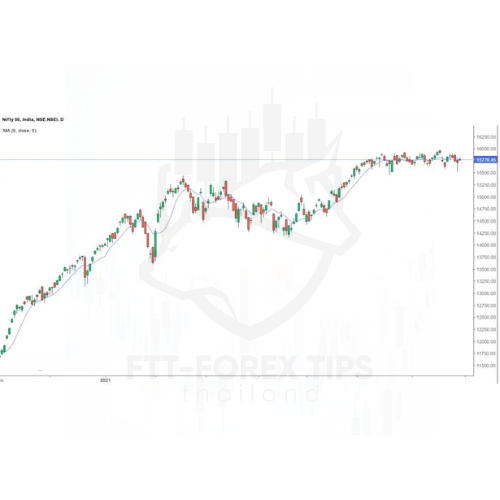
2. ค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โพเนนเชียล (EMA):
EMA เป็นค่าเฉลี่ยเคลื่อนที่อีกประเภทหนึ่งที่ให้น้ำหนักมากขึ้นกับจุดราคาล่าสุด และทำให้ตอบสนองต่อจุดข้อมูลล่าสุดมากขึ้น
EMA ตอบสนองต่อการเปลี่ยนแปลงราคาล่าสุดมากกว่าเมื่อเปรียบเทียบกับ SMA เนื่องจากใช้น้ำหนักเท่ากันกับการเปลี่ยนแปลงราคาทั้งหมดในช่วงเวลาที่กำหนด
มีสามขั้นตอนที่เกี่ยวข้องในการคำนวณ EMA:
- อันดับแรก เราต้องคำนวณค่าเฉลี่ยเคลื่อนที่อย่างง่ายสำหรับช่วงเวลาหนึ่งๆ
- จากนั้นเราต้องคำนวณตัวคูณสำหรับการชั่งน้ำหนักค่าเฉลี่ยเคลื่อนที่แบบเลขชี้กำลัง
- ขั้นตอนสุดท้ายเกี่ยวข้องกับการคำนวณ EMA ปัจจุบันโดยนำช่วงเวลาจาก EMA เริ่มต้นไปจนถึงช่วงเวลาล่าสุด โดยใช้ราคา ตัวคูณ และค่า EMA ของช่วงเวลาก่อนหน้า สูตรคือ:
EMA ปัจจุบัน = [ราคาปิด – EMA (ช่วงเวลาก่อนหน้า)] x ตัวคูณ + EMA (ช่วงเวลาก่อนหน้า)
EMA ของ 9 ช่วงเวลาสุดท้ายของ Nifty 50 ถูกพล็อตเป็นเส้นบนแผนภูมิราคาที่แสดงด้านล่าง: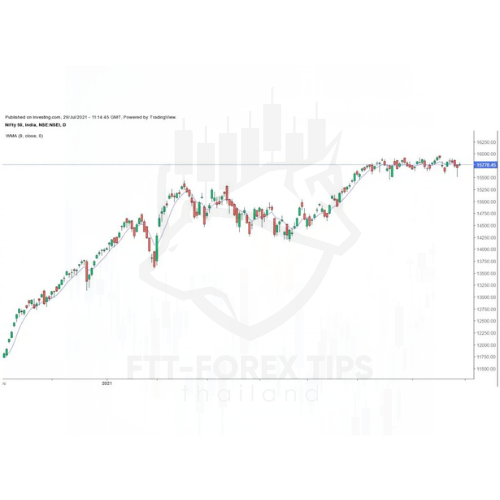
3. ค่าเฉลี่ยเคลื่อนที่ถ่วงน้ำหนัก (WMA):
WMA เป็นเส้นค่าเฉลี่ยเคลื่อนที่อีกประเภทหนึ่งที่ผู้ค้าใช้ในการสร้างทิศทางการค้าและตัดสินใจซื้อหรือขาย
โดยให้น้ำหนักที่มากขึ้นกับจุดข้อมูลล่าสุด และให้น้ำหนักที่น้อยลงในจุดข้อมูลที่ผ่านมา
คำนวณโดยการคูณแต่ละจุดในชุดข้อมูลด้วยปัจจัยถ่วงน้ำหนัก
ผู้เทรดใช้ค่าเฉลี่ยถ่วงน้ำหนักเพื่อสร้างสัญญาณการค้า ตัวอย่างเช่น เมื่อราคาอยู่เหนือเส้นค่าเฉลี่ยเคลื่อนที่แบบถ่วงน้ำหนัก มันจะส่งสัญญาณว่าแนวโน้มเป็นขาขึ้น
แต่ถ้าราคาอยู่ต่ำกว่าการถ่วงน้ำหนัก แสดงว่ามีแนวโน้มลดลง
WMA ของ 9 ช่วงเวลาสุดท้ายของ Nifty 50 ถูกพล็อตเป็นเส้นบนกราฟราคาที่แสดงด้านล่าง: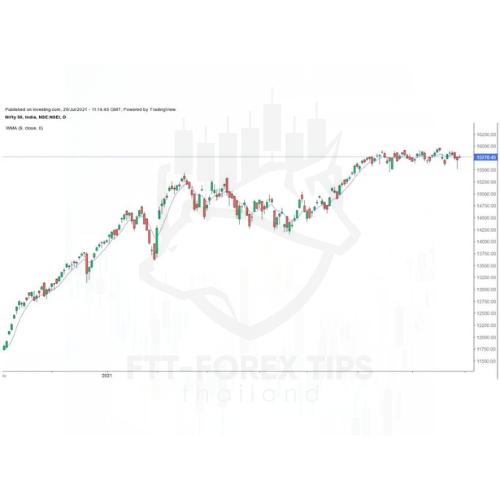
4. ค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โพเนนเชียลสองเท่า (DEMA):
DEMA เป็นเวอร์ชันปรับปรุงของ EMA เนื่องจากจัดสรรน้ำหนักให้กับจุดข้อมูลล่าสุดมากขึ้น
ช่วยลดผลแล็กและตอบสนองได้ดียิ่งขึ้น ซึ่งช่วยให้เทรดเดอร์ระยะสั้นมองเห็นการกลับตัวของแนวโน้มได้อย่างรวดเร็ว
ให้เราดูราคา Nifty 50 ใน 9 วัน: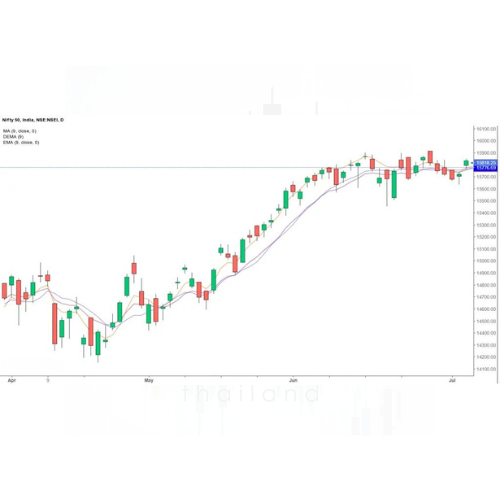
เส้นสีน้ำเงินแสดงถึงเส้นค่าเฉลี่ยเคลื่อนที่อย่างง่าย เส้นสีม่วงแสดงถึงเส้นค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โปเนนเชียล (EMA) และเส้นสีเหลืองคือเส้น DEMA
จากแผนภูมิด้านบน เราสามารถพูดได้ว่า DEMA อยู่ใกล้กับจุดราคามากที่สุดและมีค่าเบี่ยงเบนน้อยที่สุด
เนื่องจากเส้น DEMA เลียนแบบราคาหุ้นอย่างใกล้ชิดที่สุด ดังนั้นจึงมีความอ่อนไหวต่อความผันผวนของหุ้นมากที่สุด การเปลี่ยนแปลงของความผันผวนเป็นตัวบ่งชี้ที่ดีสำหรับการกลับตัวของแนวโน้ม และด้วยเหตุนี้ การซื้อขายหุ้น
5. ค่าเฉลี่ยเคลื่อนที่แบบเอกซ์โพเนนเชียลสามเท่า (TEMA):
TEMA ช่วยลดความล่าช้าของ EMA และทำให้ตอบสนองต่อราคาได้มากขึ้น
หลังจากที่ Double Exponential Moving Average (DEMA) ได้รับการพัฒนาในปี 1994 Patrick Mulloy ได้สร้าง Triple Exponential Moving Average (TEMA)
เช่นเดียวกับ DEMA TEMA จะลดความแตกต่างของความล่าช้าระหว่าง EMA ต่างๆ
ความแตกต่างระหว่าง DEMA และ TEMA คือสูตรของ TEMA ใช้ EMA ที่ราบรื่นสามเท่า นอกเหนือจาก EMA แบบเดี่ยวและแบบเรียบสองเท่าที่ใช้ในสูตรสำหรับ DEMA
ในแผนภูมิด้านล่าง TEMA จะแสดงเป็นเส้นสีเหลือง และ DEMA แสดงเป็นเส้นสีม่วง: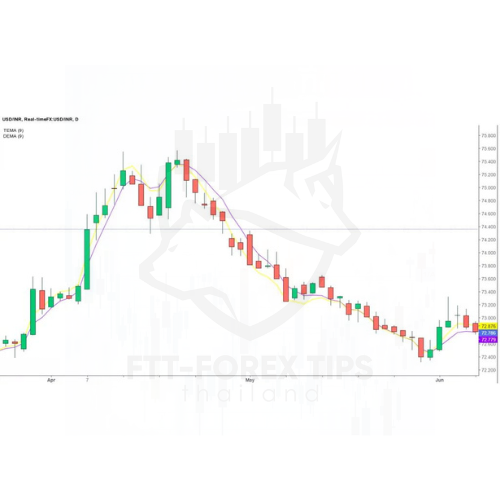
ดังนั้น อินดิเคเตอร์นี้ที่สร้างขึ้นโดยใช้ EMA ทั้งสามนี้จะสร้างเส้นค่าเฉลี่ยเคลื่อนที่ซึ่งอยู่ใกล้กับแถบราคามากกว่า DEMA
6. การถดถอยเชิงเส้น (หรือ) ค่าเฉลี่ยเคลื่อนที่กำลังสองน้อยที่สุด:
เส้นค่าเฉลี่ยเคลื่อนที่น้อยที่สุดกำลังสอง (LSMA) คำนวณเส้นถดถอยกำลังสองน้อยที่สุดสำหรับช่วงเวลาก่อนหน้า นำไปสู่การคาดการณ์ล่วงหน้าจากงวดปัจจุบัน
อินดิเคเตอร์ช่วยในการระบุสิ่งที่อาจเกิดขึ้นหากเส้นถดถอยยังคงดำเนินต่อไป
อินดิเคเตอร์จะขึ้นอยู่กับผลรวมของวิธีกำลังสองน้อยที่สุดในการค้นหาเส้นตรงที่เหมาะกับข้อมูลในช่วงเวลาหนึ่งๆ

No Comments